[THE_EXPR_METHOD] 012 Trapezoid
[THE_EXPR_METHOD] 012 トラペゾイド
ノコギリ波のように、いくつかの波形は簡単に実装ができてシグナルの操作に役立つパーツとして使うことができます。
トラペゾイド(台形)もそのような1つの例です。
それは特にアンプリチュード(音量)のエンベロープに使うのに適しています。スムーズなアタック部とディケイ部があり、エンベロープの”オン”の部分は可能な限りフルに開いた状態になったままです。例えば、もし三角波が使われていたら、エンベロープはフルに開いた状態のままにはなりません。シグナルは最高値(トップ)になった瞬間に下がっていきます。その結果、変調されたシグナルは連続的なフェードインとフェードアウトの状態か、全体的な”ラウドネス”がない状態に見えます。一方、トラペゾイドはこれらの点に対処する便利な方法を提供します。
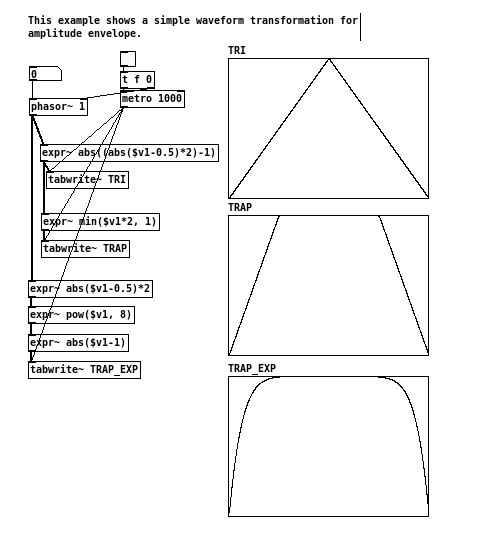
実際に、2つの操作を追加することで台形波は三角波から簡単に生み出すことができます。三角波をまず好きな量だけスケールアップ(乗算)します。それからエンベロープのY軸の最大値(通常は1.0)のところでクリップします。シグナルのスケールアップが大きいほど台形の側面の傾斜は急になり、より短いアタック/ディケイになります。
もうひとつのバリエーションはpow()関数を使ったものです。(反転した)三角波の直線的な傾斜スロープを指数曲線に変化させます。その後、そのエンベロープは正しい方向に反転して使用します(ベル型の曲線)。このメソッドの良い点は、(台形の場合と)同じブレークポイントの位置を与えられても”オン”になっているエリアが台形の場合よりも増えることです。その変調の結果として、ラウドネス(聴感上の音量)のロスがより少なく知覚されることになります。そのようなエンベロープの形は、台形よりもクラシックのチェロ(の演奏時のエンベロープ)の形に近いものです。
以前のサンプルの再生の投稿で、サウンドファイルを複数のセクションに切り分けていましたが、それらのセグメントの端の部分でゼロクロッシング(振幅が0の状態)になっていないとクリッピング(過大な振幅でノイズになること)がよく発生します。これに対してトラペゾイド(台形)波形や同等の波形を振幅(音量)のエンベロープとして使って、エラーを修正するのは理想的なシナリオです。
EXAMPLE PATCH: 012_trapezoid.pd
練習問題:
上記の例に似た、波形の変換に使える他のスロープ/カーブのタイプはありますか?
※この翻訳はChun Lee氏の[expr~]オブジェクトを使った作曲パッチの制作メソッドを和訳したものです。Chun Lee氏の許諾を得ています。
※元サイト