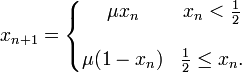カオスを聞く
カオス理論とは、予測できない複雑な様子を扱う理論のことで、これを応用すれば単純な数式からいわゆる「乱数」とも異なる数値の複雑な振る舞いを発生させたりすることができます。
カオス理論について詳しくはWikipediaなどをご覧ください。
ここではこのカオス的性質もつ数値の振る舞いの一つであるテント写像を、簡単にPdで生成する方法を紹介します。
テント写像は以下の式によって表す事ができます。
この式を簡単に説明すると、「次」の値 Xn+1 は「現在」の値、Xnが0.5以下の場合、Xnに係数μを掛けた値となり、Xnが0.5かそれより大きいときは、1からXnをひいた数にμを掛けた数となるという事です。
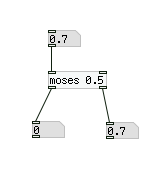
まず、最初にPdで入力された値が一定の数、(この場合0.5)より大きいか小さいかによって処理の分岐を行う場合「moses」というオブジェクトを使います。下図のようなパッチを作り、上のナンバーボックスに0.5より大きい数、それより小さい数を入れてみてください。それぞれ0.5より小さい数は左、0.5以上の数は右のインレットから出力されるはずです。以下の例では0.7という0.5以上の数を入力したので、それが右アウトレットから出力されていますが、0.3など0.5より低い数値を入れた場合は左インレットからそれが出力されます。
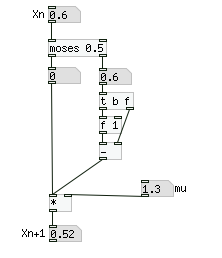
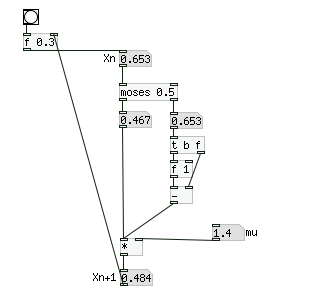
式によると現在の値が0.5より小さい場合は単純にμと現在の値を掛けるのみ、0.5以上の場合はまず1から現在の値を引いて、それにμを掛けることになります。これをPdでプログラミングすると以下のようになります。
次に以下のように「bng」を押すたびに「次」の値が「今」の値に代入される仕組みを作ります。
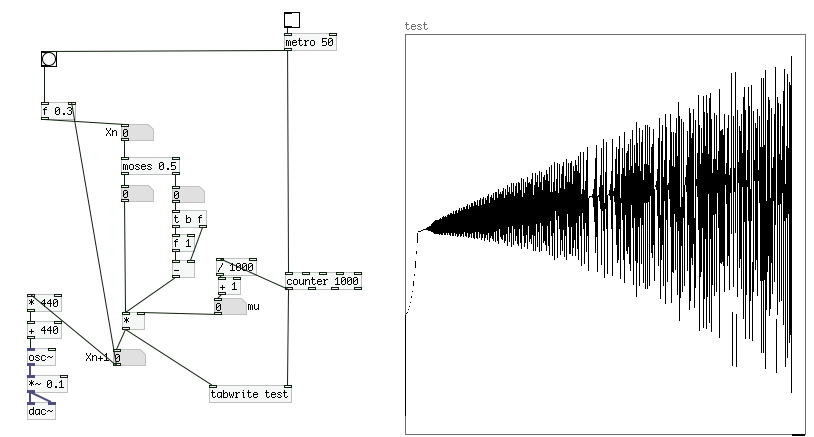
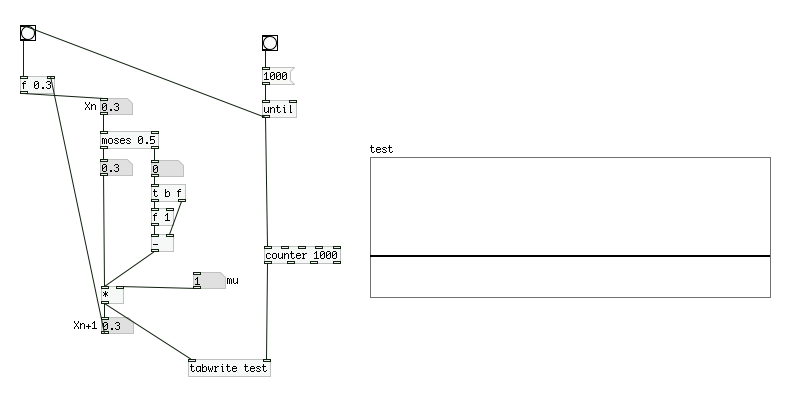
テント写像ではμの値が1より大きく2以下の時は多周期軌道を描きます。このルーチンの出力する値の振る舞いがμの値を変える事によってどのように変化するのかをArrayを使って記録してみましょう。以下の例では「until」オブジェクトによってbangを瞬時に1000回出力し、tabwriteを使って、ルーチンが出力した値をArrayに書き込んでいます。
(尚、「現在」の値の初期値として0.3を用いています。)
μの値を変えると、出力される値の範囲が変わります。
μ= 1.1

μ= 1.5
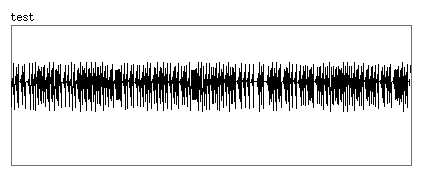
μ= 1.9
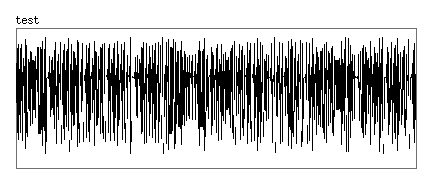
このμの値を1から2まで徐々に変えていったのが以下です。だんだん値の範囲が大きくなっていっています。
次はこれを音として聞いてみましょう。Xn+1の値を440倍し、その値に440を足し、A4のA5の音高のパラメータにテント写像の出力値をマップし、metroによって出力値一つ一つを50ミリ秒ずつ聞けるようにします。
最初はグリッサンドが聞こえ、ある音高にとどまり、それからそれが2つの音高を反復するパターンに聞こえるようになり、そしてある地点からアルペジオのように聞こえ、最終的にランダムに聞こえるような状態に入ります。このようにカオスを応用すれば、単純なパラメータの変化で様々なパターンを作り出すことができます。