アナログ・モデリングFM
我々が今まで作ってきたFM関係のプログラムは全て、リニアFMと呼ばれるものです。
キャリア周波数があり、それに対してモジュレータが変調を加えると、キャリア周波数に対し等間隔、対称的にサイドバンド群が並びます。これをリニアFMといいます。しかし、アナログ・シンセのFMのサイドバンド群は等間隔・対称的には並ばない事があります。
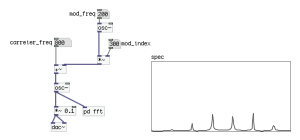
なぜこんな事がおこるのかというと、人間の音高に対する知覚が指数関数的であるのに関係があります。例えば、ピアノの真ん中のラ(A4)の周波数は440Hz.ですが、1オクターブ下(A3)のラは220 Hz、1オクターブ上のラ(A5)は880 Hz.です。なのでA3とA4は220 Hz.の差がありますが、A4とA5は440 Hz.の差があります。しかし、我々はA3とA4、A4とA5の距離を「等間隔」、同じオクターブの音程と知覚します。

この人の知覚に合わせて、アナログ・シンセは、今まで勉強してきた等間隔にサイドバンドを立てるリニアFMに対し、指数関数的にサイドバンドが立つ、「指数的(exponential)FM」を行うことがあります。もし、このアナログ・シンセのFMをPdでエミュレーションするとするならば「motf~」を使うのが手っ取り早い方法です。
以下の例ではMIDIノートナンバー69(=440Hz.)に対し、12(=1オクターブ)の振幅で変調をかけ、それを「ftom~」で周波数に変換しています。Array「exp」はこのモジュレータがキャリアに対してどのように変調をかけているかをプロットしたものです。見てわかるように波は880 Hzと220 Hz.の間を行き来していますが、上下が非対称的で、220 Hz – 440 Hzの変化は緩やかですが、440 Hz. 880 Hz間は若干とんがっています。
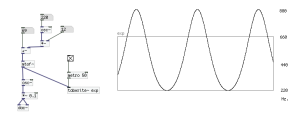
以下のように、リニアFMのものと比べるとその差は明らかです。
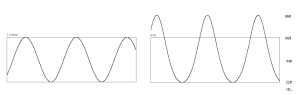
聴感上、指数的FMは変調指数を上げていくと、中心の音高が定まらなく聞こえます。これも指数的FMの特性です。指数的FMでは中央周波数を変えずに変調指数だけ上げる事ができないのです。しかし、この音程が狂って聞こえる音がアナログ的な音の「味」ともいえます。12音平均律上の楽器として考えると使い勝手が悪いかもしれませんが、一種の効果と考えるとこのアプローチもまた面白いかもしれません。
(参考: Curtis Roads, The Computer Music Tuturial)